Est-ce que la pensÃĐe a un effet sur la pourriture du riz ?

RÃĐalisation de lâexpÃĐrience dâEmoto qui consiste à savoir si notre pensÃĐe et notre volontÃĐ peut avoir une influence sur la matiÃĻre.
Date de publication : 13/03/22
Introduction
Masaru Emoto (1943 - 2014) ÃĐtait un homme dâaffaires et un auteur qui affirmait que la conscience humaine affecte la structure molÃĐculaire de lâeau. Il a proposÃĐ dans un livre une expÃĐrience à ses lecteurs pour tester son hypothÃĻse : cuire du riz et en mettre une partie dans un pot à aimer et une autre partie dans un pot à dÃĐtester. Le pot de riz aimÃĐ ne doit pas pourrir contrairement à un riz dÃĐtestÃĐ [1]. On voit une scÃĻne dans le film "les petits mouchoirs (2010, Guillaume Canet)" qui aborde ce sujet et ainsi propage cette croyance. Cette idÃĐe de pouvoir avoir une influence par la pensÃĐe donne de lâespoir, et la façon dont notre volontÃĐ seule peut magiquement amÃĐliorer la santÃĐ ou guÃĐrir une maladie serait rÃĐvolutionnaire. Ces idÃĐes, mÃĐlangÃĐes à des pseudo-sciences en mÃĐdecine, sont largement rÃĐpandues dans la population [2-5] malgrÃĐ leur manque dâefficacitÃĐ dÃĐmontrÃĐe [4-9]. Jâai eu envie de tester cette hypothÃĻse, devenue croyance, qui est finalement simple à vÃĐrifier et il faut bien le dire tout le monde à envie dây croire.
Question : La conscience peut-elle augmenter ou ralentir de maniÃĻre significative le nombre de moisissures sur le riz ?
Mon hypothÃĻse : Les moisissures ne devraient pas augmenter significativement dans un groupe ou un autre au seul motif de la pensÃĐe qui est attribuÃĐe.
Mon expÃĐrience : RÃĐaliser une expÃĐrience randomisÃĐe en double aveugle oÃđ les ÃĐchantillons de riz sont soit aimÃĐs soit dÃĐtestÃĐs. Suivre le nombre dâÃĐchantillons pourris, le nombre de moisissures sur chaque ÃĐchantillon et leur surface.
Variables indÃĐpendantes : Lâenvironnement ÃĐmotionnel du riz (certains sont insultÃĐs, dâautres sont soumis à des louanges).
Variables contrÃīlÃĐes : Un environnement similaire pour chaque ÃĐchantillon (tempÃĐrature, humiditÃĐ, exposition à la lumiÃĻre).
Variables dÃĐpendantes : Le nombre et la surface des moisissures.
MatÃĐriel et mÃĐthodes
MatÃĐriel : 2*250ml de riz (PrestoÂŪ) ; 2*250 ml dâeau (BahiaÂŪ) ; BÃĐcher de 1L ; Plaque chauffante ; Des ÃĐlÃĻves de 4ÃĻme et des collÃĻgues ouverts dâesprit ; 2 expÃĐrimentateurs ; 40 pots dâÃĐchantillons ; 2 bacs ; Film de paraffine.
Mise en bouche
PrÃĐparation des bacs sur lesquels sont mis les ÃĐchantillons.
- Assigner au hasard une position de chaque ÃĐchantillon dans deux bacs (programme Python 1)
- PrÃĐparer les bacs avec toutes les positions
- NumÃĐroter les pots dâÃĐchantillons de 1 à 40
CODE PYTHON 1
import math;
import random;
total = list(range(1, 41));
ordrerangement = random.sample(total, 40);
print("ordre des pots sur la tableâ : ",(ordrerangement));
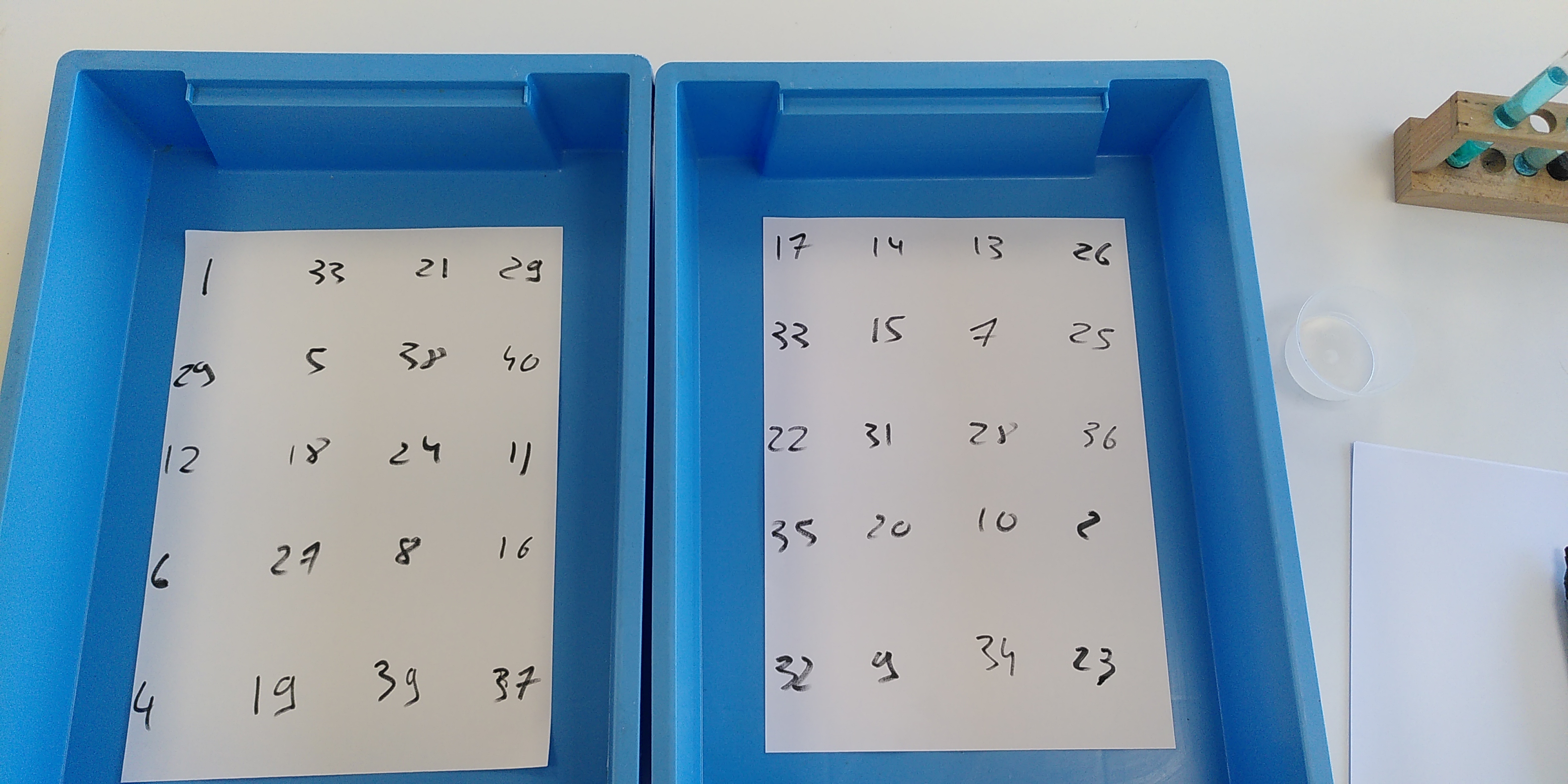
PrÃĐparation dâun bac à ÃĐchantillons

NumÃĐrotation des pots à ÃĐchantillons
Plat de rÃĐsistance : Cuisson du riz, AKA "wok culture"
- Faire bouillir 250ml dâeau dans un bÃĐcher de 1L
- Faire cuire 250ml de riz dans lâeau pendant 10 minutes
- Garder le riz chaud (contrÃīler la tempÃĐrature)
- Remplir le fond de chaque pot dâÃĐchantillon de 1 à 20, avec un maximum dâune couche de grains de riz.
- Couvrir les ÃĐchantillons avec un film de paraffine
- Placer les ÃĐchantillons à la position assignÃĐe par le programme python dans les bacs
- Recommencer tout le processus pour le 21ÃĻme au 40ÃĻme pot.

ExpÃĐrimentateur 1

Remplissage des pots à ÃĐchantillons

 Ãchantillons de riz placÃĐs à leur position assignÃĐes au hasard.
Dessert : The rise of pourritures pendant 2 semaines
- (ExpÃĐrimentateur 2) Attribuer au hasard une humeur (haine/amour) pour chaque ÃĐchantillon (programme Python 2) et cacher cette liste à lâexpÃĐrimentateur 1
- Consigner les ÃĐchantillons de chaque groupe sur une feuille à lâabri du regard de lâexpÃĐrimentateur 1
- Faire aimer ou dÃĐtester chaque jour chaque pot individuellement, avec conviction, en fonction de leur affectation prÃĐcÃĐdente consignÃĐe sur la feuille. RÃīle à donner à des collÃĻgues un peu timbrÃĐs ou des ÃĐlÃĻves convaincus
- Placer et retirer lâÃĐchantillon du bac pendant le transfert de sentiments
- Quotidiennement, tourner de 90° les bacs dâÃĐchantillons
- ExpÃĐrimentateur 1 : compter le nombre de moisissures et la surface des moisissures de chaque ÃĐchantillon (Ã lâaveugle : expÃĐrimentateur 1 ne sait pas qui est qui)
CODE PYTHON 2
import math;
import random;
total = list(range(1, 41));
jetaimeliste = random.sample(total, 20)
print("liste de pot âje tâaimeâ : ",(jetaimeliste));
jetedeteste = [x for x in total if (x not in jetaimeliste)];
print("liste de pot âje te detesteâ : ",(jetedeteste));

Une gentille ÃĐlÃĻve de quatriÃĻme transmet ses ÃĐmotions, uniquement de lâamour jâen suis sÃŧr

Comptage quotidien de moisissures, ici #17. A ce moment lâexpÃĐrimentateur 1 ne connait pas la nature des ÃĐmotions envoyÃĐes à chaque ÃĐchantillon
Digestion : La riz-vÃĐlation
Enfin, compiler les donnÃĐes et rÃĐvÃĐler riz est riz (qui est qui).

La feuille secrÃĻte donnÃĐe aux transmeteurs.trices dâÃĐmotions
Observations
- AprÃĻs quelques jours, les moisissures peuvent fusionner. Le nombre de taches fusionnÃĐes rapportÃĐes dans ce cas reste le mÊme que prÃĐcÃĐdemment, seule la surface change.
- Les moisissures foncÃĐes et vertes sont les plus faciles à repÃĐrer. Parfois, des moisissures jaunes apparaissent plus tard.
- Le riz a ÃĐtÃĐ aimÃĐ ou dÃĐtestÃĐ dans diffÃĐrentes langues et avec diffÃĐrentes intensitÃĐs : friz-çais (français), arizb ou dariz-ja (arabe - Darija marocaine), riz OlÃĐ (espagnol).
InterprÃĐtations [10-12]
Jâai effectuÃĐ un test statistique, lâanalyse de survie de Kaplan Meier (non paramÃĐtrique). Ce test est rÃĐalisÃĐ pour rÃĐpondre à la question H0 : les 2 groupes sont-ils identiques ? La rÃĐponse à cette question est une p-value. Plus la valeur p est grande, plus elle rÃĐpond oui à H0 avec certitude.
Lâanalyse de survie rÃĐvÃĻle une valeur p de 0,87. Il nây a pas dâeffet sur lâapparition de moisissures en fonction du groupe (aimÃĐ/ dÃĐtestÃĐ), mÊme conclusion avec le test Log-Rank dont la valeur p est de 0,86.
Nous sommes pratiquement sÃŧrs que les deux groupes sont ÃĐgaux avec respectivement 87 et 86 % de certitude. Le nombre dâÃĐchantillons touchÃĐs par la moisissure nâest pas significativement diffÃĐrent entre les deux groupes (n = 40).
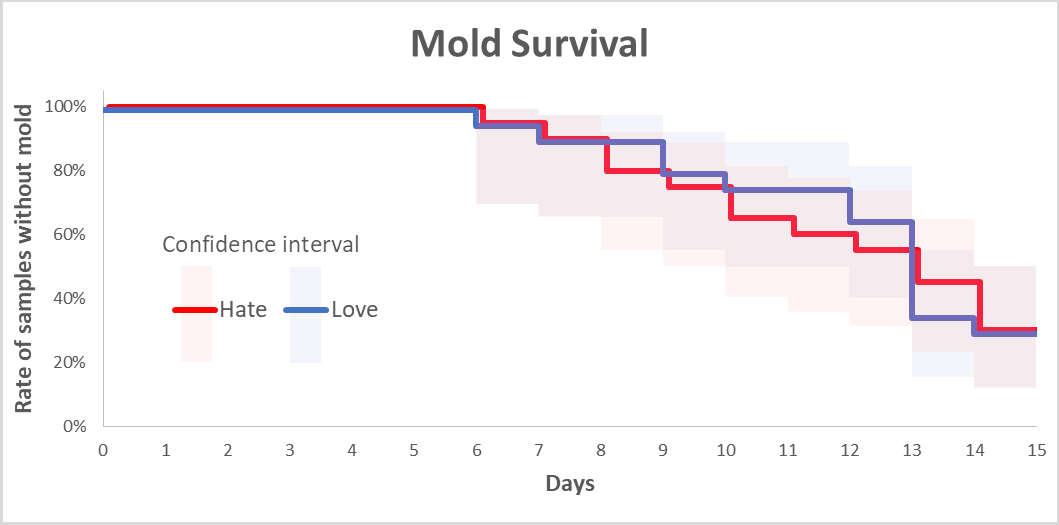
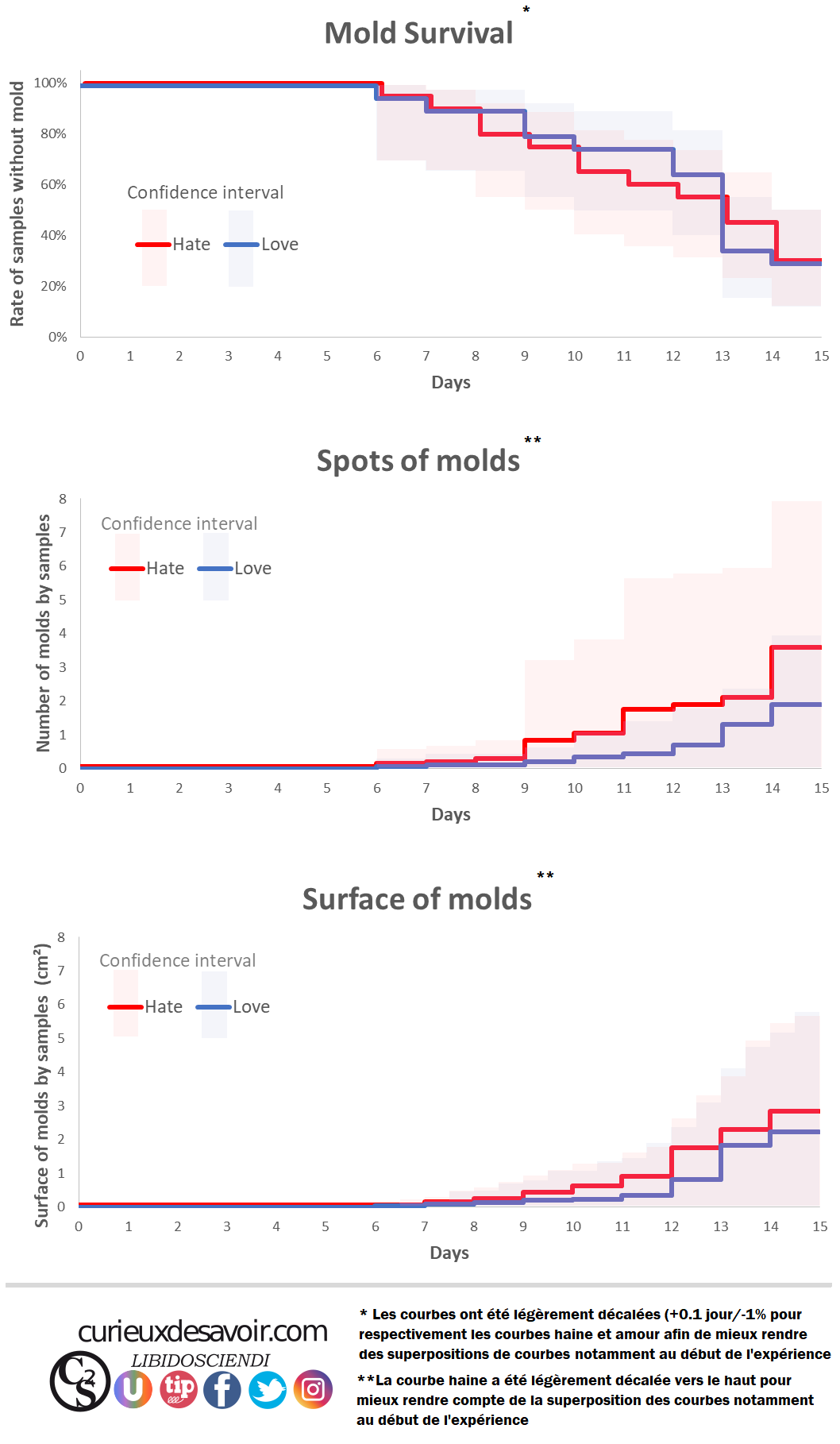
Test de Survie. En bleu le pourcentage de pots aimÃĐs sans moisissure visible, en rouge le pourcentage de pots dÃĐtestÃĐs sans moisissure visible. La courbe reprÃĐsente lâÃĐvolution du pourcentage de chaque pot en fonction du temps en jours. Les carrÃĐs rouge et bleus reprÃĐsentent lâintervalle de confiance, câest à dire la variation de pourcentage possible si lâon tient compte des erreurs et de la variabilitÃĐ des ÃĐchantillons. Chaque groupe pourrait Être soit au dessus soit en dessous des courbes dans ces carrÃĐs, avec une confiance de 95%. Les incertitudes des deux groupes se recoupent, voulant dire que chaque groupe pourrait Être inversÃĐ, aucun groupe nâatteint une valeur significative dan sun sens oÃđ lâautre.
AprÃĻs 14 jours, on compte 14 pots aimÃĐs impactÃĐs par la moisissure et 14 pots dÃĐtestÃĐs impactÃĐs par la moisissure (le jour 15 a ÃĐtÃĐ ajoutÃĐ sur le graphique afin de mieux voir les rÃĐsultats du jour 14).
Le test de Kruskal-Wallis (non paramÃĐtrique) pour chaque jour sur le nombre de taches et leur surface. Une valeur p > 0,05 rejette lâhypothÃĻse dâune diffÃĐrence entre les deux groupes. Jamais une diffÃĐrence significative entre les deux groupes nâa ÃĐtÃĐ dÃĐtectÃĐe.
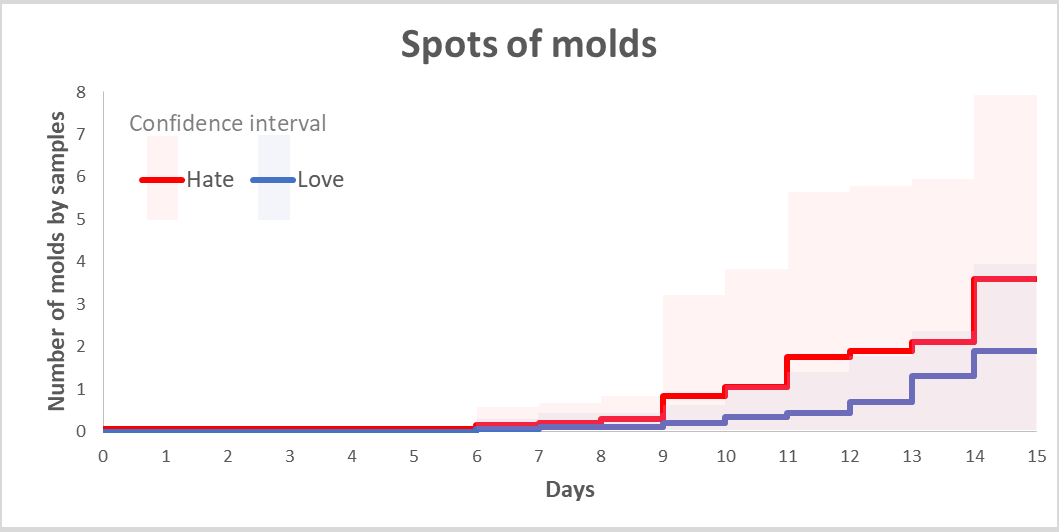
Nombre moyen de points de moisissure dans le groupe aimÃĐ (bleu) et dÃĐtestÃĐ (rouge). Si le nombre de spot nâest pas identique, il nâest PAS significativement diffÃĐrent. Les intervalles de confiance des deux gorupes se croisent. (le jour 15 a ÃĐtÃĐ ajoutÃĐ sur le graphique afin de mieux voir les rÃĐsultats du jour14).
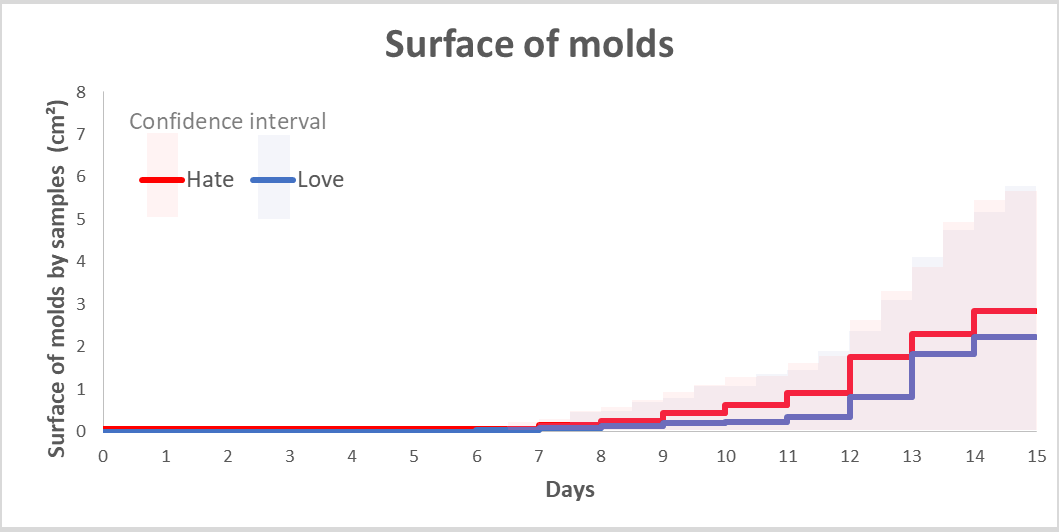
Surface moyenne de moisissure dans le groupe aimÃĐ (bleu) et dÃĐtestÃĐ (rouge). Si la surface de moisissure nâest pas identique, elle nâest PAS significativement diffÃĐrente. Câest à dire que la surface de moisissure statistiquement identique entre les deux groupes (le jour 15 a ÃĐtÃĐ ajoutÃĐ sur le graphique afin de mieux voir les rÃĐsultats du jour14).

Tests statistiques pour tous les jours

Exemples de pots : #18 ÃĐtait un dÃĐtestÃĐ
Conclusion
LâhypothÃĻse dâEmoto ÃĐtait rizible mais nâest pas validÃĐe par notre expÃĐrience. AprÃĻs 14 jours, aucune diffÃĐrence significative entre les 2 groupes dâÃĐchantillons de riz (20 haÃŊs-20 aimÃĐs) nâest observÃĐe quelles que soient les variables :- AprÃĻs 14 jours dâaffilÃĐ, le nombre dâÃĐchantillons touchÃĐs par la moisissure : pas de diffÃĐrences, p-value : 0,87>>0,05 (test de Kaplan Meier) 0,86>>0,05 (test de Log Rank).
- Nombre quotidien de taches de moisissure : aucune diffÃĐrence, p-value : 0,36-1 >>0,05.
- Surface quotidienne de moisissures : pas de diffÃĐrence, p-value : 0,39-0,99 >>0,05.
Cette expÃĐrience a mis en ÃĐvidence lâimportance dâune expÃĐrience randomisÃĐe en aveugle [15,16], notamment en raison dâun nombre ÃĐlevÃĐ de paramÃĻtres et dâune forte variabilitÃĐ intergroupe. En effet il est certain quâavec la connaissance des ÃĐmotions attribuÃĐes aux ÃĐchantillons, on aurait tendance à biaiser nos observations. Quoi quâil en soit, cette expÃĐrience fut trÃĻs en-riz-chissante.
AmÃĐliorations possibles
"La dÃĐmarche scientifique"
- Un contrÃīle plus poussÃĐ de lâhumiditÃĐ (facteur important dans la croissance des moisissures)
- Un contrÃīle de la contamination initiale par des moisissures (contamination volontaire)
- Un comptage plus prÃĐcis des moisissures (ex : qPCR)
- Plus dâÃĐchantillons
- Ou simplement arrÊter de perdre du temps dans des expÃĐriences dont on connait dÃĐjà les rÃĐsultats [21]...
"Je veux croire"
- Plus dâÃĐtudiants contrariÃĐs lÃĒchant leur haine sur le riz (par exemple aprÃĻs une mauvaise note)
- Veiller à parler dans la mÊme langue que le riz
- Utiliser un riz biologique complet issu du commerce ÃĐquitable
- Sâassurer des intentions des expÃĐrimentateurs avec une "ÃĐchelle de sincÃĐritÃĐ"
- Discuter avec les deux groupes de riz à au moins 123,666 m de distance pour ÃĐviter les interfÃĐrences (etc.)
- On peut trouver toutes sortes de choses sans aucun sens pour rejeter lâÃĐvidence
Post conclusion
Avec cette expÃĐrience, je voudrais montrer quâil est facile de tester une hypothÃĻse plutÃīt que de simplement y croire. Bien entendu certaines expÃĐriences sont plus faciles à mener que dâautres.
Aussi, une expÃĐrience est toujours soumise à des ÃĐvÃĐnements inattendus, des problÃĻmes et des amÃĐliorations possibles. La dÃĐmarche scientifique est toujours en recherche dâamÃĐlioration. Ainsi, nous pouvons avoir plein de questions et dâidÃĐes pour amÃĐliorer ou critiquer ce test sur le riz et les ÃĐmotions. Il faudrait garder le mÊme niveau de scepticisme, que lâon aime ou non les conclusions dâune expÃĐrience. Imaginez si jâavais fait le comptage sans Être en aveugle, enlevÃĐ des pots de riz, comptÃĐ diffÃĐremment les deux groupes, ou encore extrapolÃĐ la moitiÃĐ de mes rÃĐsultats. Pas trÃĻs sÃĐrieux. Pire si dans un an jâannonce que le nombre de pots pourris nâest pas vraiment celui indiquÃĐ.
Pensez à ces critiques, et imaginez maintenant lors dâune ÃĐpidÃĐmie mondiale, quâun druide fasse la promotion dâun remÃĻde miraculeux [17]. Imaginez sa conclusion basÃĐe sur une ÃĐtude avec seulement 6 patients dans le groupe test, aprÃĻs lâÃĐlimination dâun mort et de 3 patients gravement malades. Imaginez cette soit disant guÃĐrison comparÃĐe à un groupe de contrÃīle basÃĐ sur des donnÃĐes incomplÃĻtes et extrapolÃĐes recueillies avec une technique diffÃĐrente. LâÃĐtude est validÃĐe par un journal ami en moins de 24h (lien). MalgrÃĐ la faiblesse de cette ÃĐtude non randomisÃĐe et pas rÃĐalisÃĐe en aveugle, imaginez enfin ce remÃĻde fortement promu par ses auteurs, certains politiques ou certains mÃĐdias ignorant les alertes de la communautÃĐ scientifique mondiale. Impossible que cela nâexiste.
Heureusement quâil ne sâagit que dâune situation hypothÃĐtique, et quâaucune vie nâest en jeu. Bien entendu tout le monde serait aussi critique face à cette ÃĐtude que sur mon expÃĐrience avec le riz. Bien entendu, si un an plus tard, les auteurs admettent dans une publication en rÃĐalitÃĐ 2 morts avec leur protocole, portant le taux de lÃĐtalitÃĐ Ã 12% pour leur protocole miracle contre 0% dans le groupe contrÃīle [18]... Alors là , il en serait fini de cette pseudo-star de Youtube. Pas besoin de trois doctorats pour voir le problÃĻme.
Le comitÃĐ dâÃĐthique du CNRS a soulignÃĐ dans son rapport que les scientifiques ne devraient pas promouvoir le "populisme scientifique" pendant une crise, mais plutÃīt aider les gens à dÃĐcider (politique, mÃĐdias, citoyens) [19]. Un grand nombre dâÃĐtudes mettent en ÃĐvidence un risque de mortalitÃĐ plus ÃĐlevÃĐ associÃĐ aux pseudo-sciences et aux croyances non prouvÃĐes plutÃīt quâau recours à une mÃĐdecine fondÃĐe sur des preuves [20-22].
Exemple dâune ÃĐtude bien trop faible pour le bruit quâelle a pu faire et le melon de ses auteurs
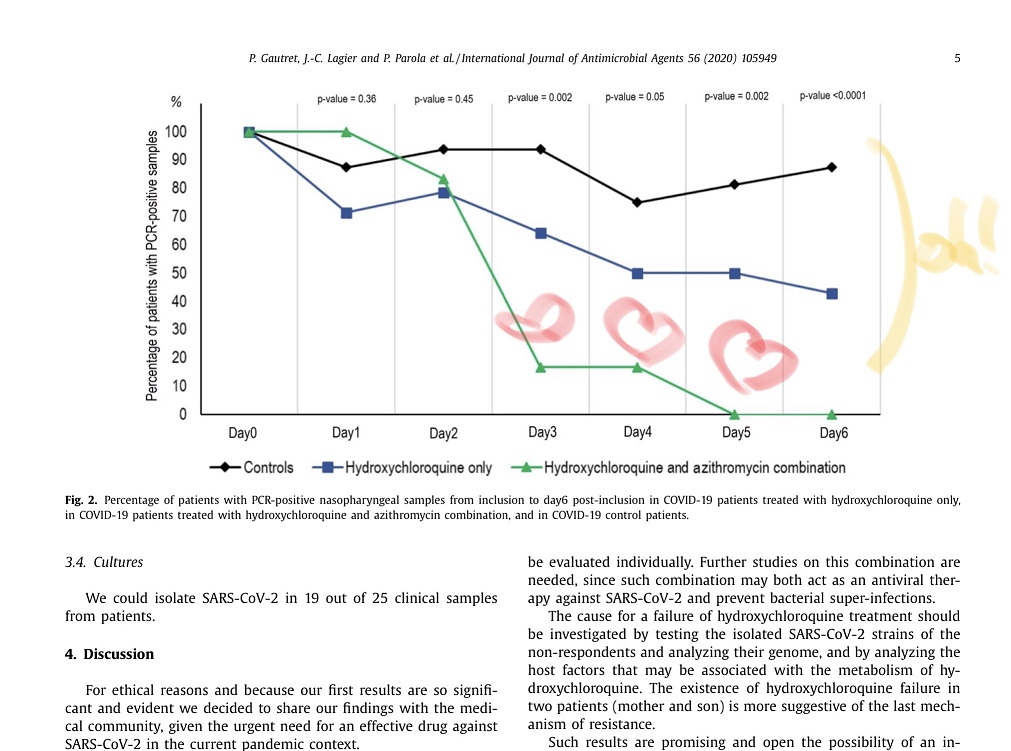
RÃĐsultat impressionnant qui donne un ÃĐnorme espoir
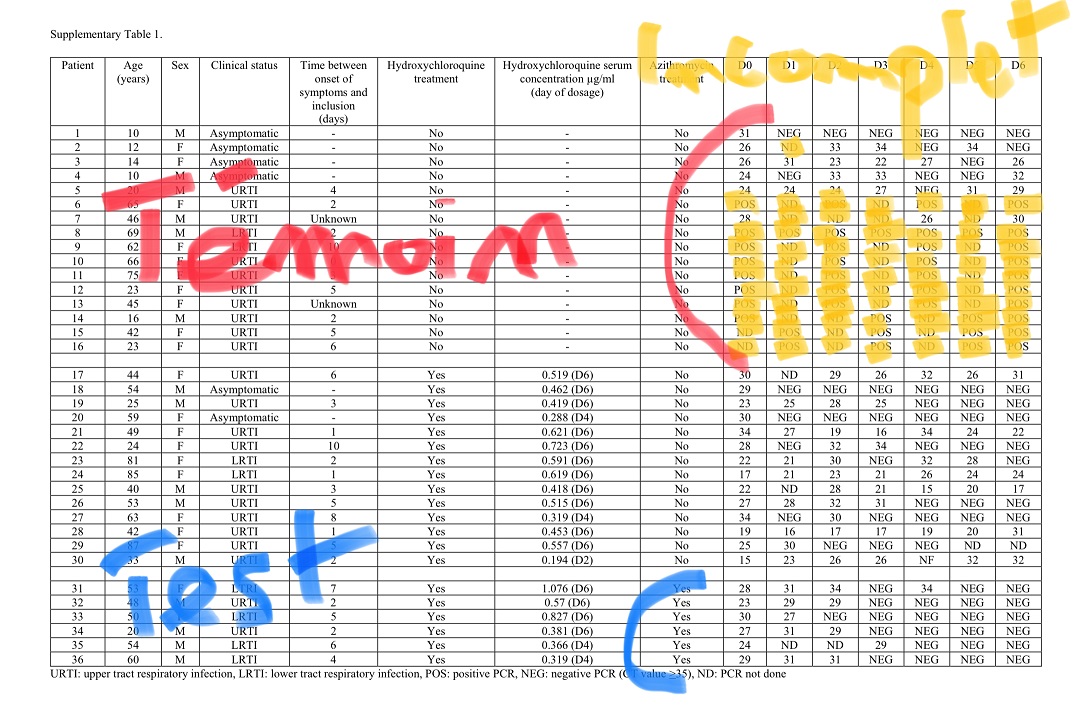
Il semblerait que prÃĻs de 60% des donnÃĐes sur le groupe contrÃīle soient manquantes, et donc ont ÃĐtÃĐ extrapolÃĐes.

Exemple fictif suite... Comment supprimer des morts et malades graves dâune ÃĐtude pour conclure que le remÃĻde est miraculeux.

Seconde publication fictive de la mÊme ÃĐquipe de recherche qui finalement montre que son groupe qui prend son remÃĻde miraculeux montre 12% de mortalitÃĐ, 6% dans son demi remÃĻde et 0% dans le groupe contrÃīle dâun autre hÃīpital trop mauvais à la botte de big pharma qui ne travaille pas bien.
Conflits dâintÃĐrÊts
Lâauteur ne dÃĐclare aucun conflit dâintÃĐrÊt (sauf une prÃĐfÃĐrence pour le couscous plutÃīt que le riz). Lâauteur ne dÃĐclare aucun retrait dâÃĐchantillons ou de donnÃĐes non dÃĐsirÃĐs.
La bibliographie est accessible grÃĒce à sci-hub, sci-hub supprime les obstacles à la science et donne de meilleurs sources que Youtube.
PhosphorÃĐ par : Gontier Adrien
Mots clefs : Riz, Emoto, COVID