Comment gagner aux jeux de grattage ?

Voici la méthode miracle pour gagner aux jeux de grattage, méthode concoctée par un célèbre médium marabout. A défaut de miracle, comprenez les méthodes de calcul des gains espérés pour les cartes à gratter, pourquoi sommes-nous attirés par le jeu et le poids de ce dernier auprès des personnes dépendantes.
Date de publication : 18/08/16
Jeux de hasard et jeux de grattage
Les jeux de hasard sont constitués, aujourd’hui, de plusieurs sous-types de jeux :
- Les jeux dits de « tirage », comme le Loto ou l’Euro-Million, qui consistent à parier sur la sortie d’une série de chiffres tirés a posteriori par la société de jeux.
- Les paris, qui consistent à parier sur les résultats sportifs de jeux comme le football, de combats comme la boxe ou encore sur l’arrivée d’une course de chevaux ou de lévriers.
- Les jeux dits de « grattage » ou « instantanés » comme le « Black Jack », « l’Astro » ou le « Bingo ». Ces jeux de hasard, tous regroupés sous la marque « Illiko » en France, consistent à gratter une ou plusieurs parties d’un ticket pour découvrir le gain obtenu.
Les jeux de grattage ont un faible coût et offrent, le cas échéant, un gain immédiat. Ils sont de plus en plus prisés1 et c’est donc à ces jeux que nous nous intéresserons.
Rappel Historique
Les jeux de hasard ont fortement évolué au cours du temps, que ce soit au niveau de leur forme (dés, cartes, osselets) au niveau des enjeux (parcelles de terrain dans l’Ancien Testament, prédire l’avenir en Extrême Orient, attribution de places de marché au XIIIème siècle à Bruxelles) ou encore au niveau de leur statut (illégaux dans de nombreux pays comme la Corée aujourd’hui ou en France jusqu’au XVIIème siècle2). Autant dire que les jeux de hasard sont presque aussi vieux que les civilisations.
En France, c’est à l’aide de la Loterie Royale en 1658 que fut financé l’Hôpital Général de Paris3, aujourd’hui appelé « Salpêtrière ». La Française des Jeux (FDJ) succèdera à la Loterie nationale en 1976, laquelle finançait des aides aux anciens combattants ou encore aux agriculteurs sinistrés. Les entreprises de jeux se révèlent bien souvent publiques : en France, l’Etat possède 72% des parts de la FDJ.
Dans le monde, les ventes de jeux de hasard (loto, cartes à gratter) représentent un marché important (220 milliards de dollars en 20074). A titre d’exemple, en France, l’équivalent de 87 millions d’euros sont dépensés chaque jours en jeux de hasard, ce qui équivaut à un Airbus A321 Neo1. Une proportion importante et variable de joueurs réguliers ou occasionnels tente leur chance : jusqu’à 70% d’espagnols jouent au moins une fois par an comparé à 40 % d’allemands5.
Un jeu pour perdre : les probabilités
Afin de bien appréhender les chances de gains et de pertes lors des jeux de hasard (grattage, dés, loteries etc.) il faut aborder les probabilités. Les notions de probabilités répondent à des règles mathématiques très strictes, mais assez simples. Comme nous allons le voir par la suite, notre sens de la logique peut très mal appréhender ces règles pourtant rationnelles.
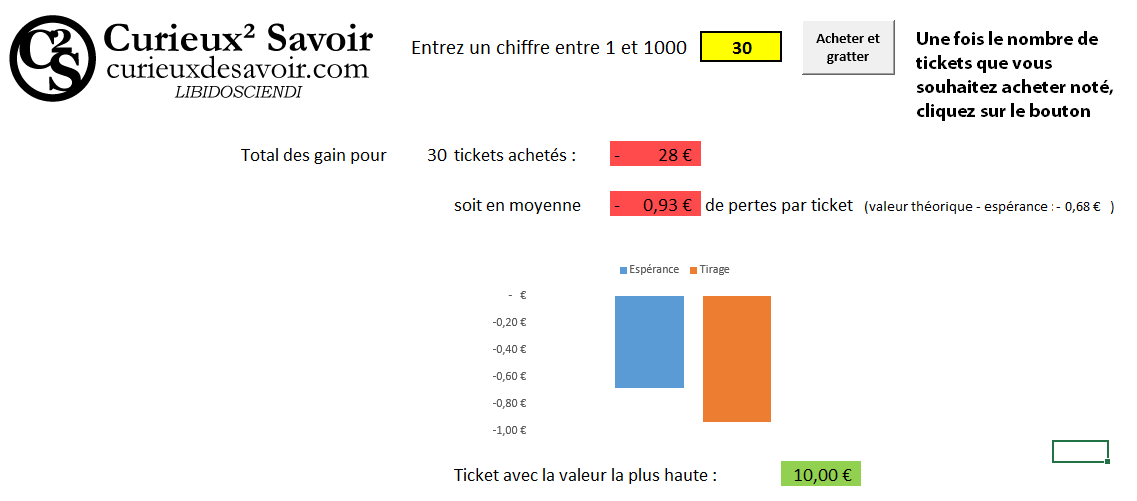
La française des Jeux a l’obligation de noter au dos des jeux à gratter le nombre de tickets imprimés ainsi que le nombre de lots gagnants avec leurs gains respectifs. Au jeu de grattage « Black Jack », par exemple, on compte 50 000 tickets gagnants à 10€ sur un total de 1 500 000 tickets. On peut connaître la probabilité d’acheter un ticket gagnant à 10€ en faisant le rapport « nombre de tickets gagnants à 10€ »/« nombre total de tickets». Si on multiplie le résultat par 100 on obtient le pourcentage de chances de gagner les 10€. On a donc 3,3% de chance d’avoir ce ticket gagnant à 10€ quand on achète un ticket de Black Jack. Si on prend en compte l’achat de la carte à 2€, le gain total pour le joueur tombe alors à 8€. Théoriquement, lors de l’achat de 100 tickets, 3 seront des gagnants à 10€. Il est possible d’acheter un seul ticket et de gagner 10€ tout de suite, ou de jouer toute sa vie et de ne jamais l’avoir. Mais plus on joue, plus on s’approche d’une chance de 3,3% d’avoir des tickets gagnants à 10€. C’est le principe d’un tirage à l’infini dans le calcul des probabilités. Un principe qui est souvent mal compris.
Pour illustrer cette notion de tirage à l’infini, nous avons créé un petit modèle informatique pour jouer au jeu « pile ou face ». La probabilité d’obtenir « pile » est de 50%. Une simulation de 2 tirs nous donne 2 piles, soit pile dans 100 % des cas. On continue à tirer les dés. Avec 10 tirs simulés, pile est apparu dans 30% des cas. On est donc assez loin de la probabilité théorique (50%) et on pourrait presque croire que la probabilité calculée est fausse. Avec 40 tirs, on a obtenu pile dans 47,5% des cas, contre 51,1% avec 10 000 tirs et 50,4% avec 20 000. On remarque donc que plus on tire les pièces, plus les résultats de nos expériences se rapprochent globalement de la probabilité théorique. Globalement, car comme on peut le voir il existe des fluctuations mais la tendance amène nos tirs globaux à se rapprocher de 50% de piles et 50% de faces.
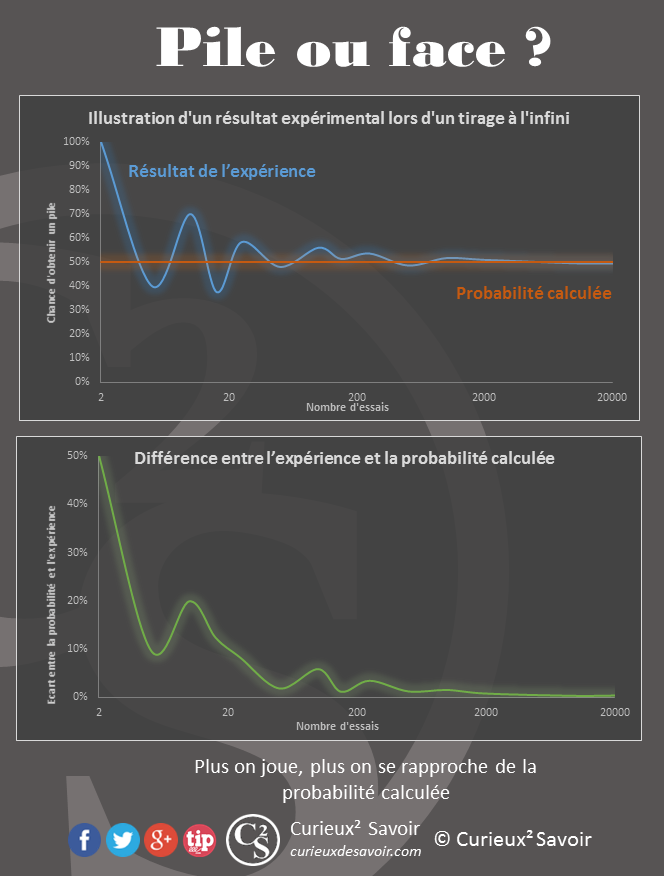
Vers l’infini et au-delà
Les sociétés de jeux sont clairement dans cette situation d’achats infinis au regard des millions de tickets vendus au loto, par exemple. Mais dans le cas des tickets de grattage elles connaissent à l’avance les gains escomptés.
Espérance
Nous arrivons à la notion d’espérance mathématique. L’espérance répond à la question : « quand on achète un ticket, quel est le gain qu’on peut espérer ? ». Pour cela on additionne l’ensemble des gains (lots proposés) et des pertes (dépense pour l’achat de chaque carte) que l’on divise par le nombre total de tickets. Il en ressort que l’espérance d’un ticket de « Black Jack » est de -0,68€. Donc, statistiquement, à chaque fois que vous achetez un ticket de black Jack, vous perdez en moyenne 68 centimes. Cela est d’autant plus vrai lorsque vous jouez beaucoup.
On peut additionner les gains que la Française des Jeux distribue au black jack et ceux qu’elle reçoit par les achats de tickets. Sur une série de 1,5 millions de tickets, le gain net de la FDJ est de 1 019 924€, et ce malgré les 1 980 076 € redistribués aux joueurs. La française des jeux est donc gagnante dans 100% des cas.
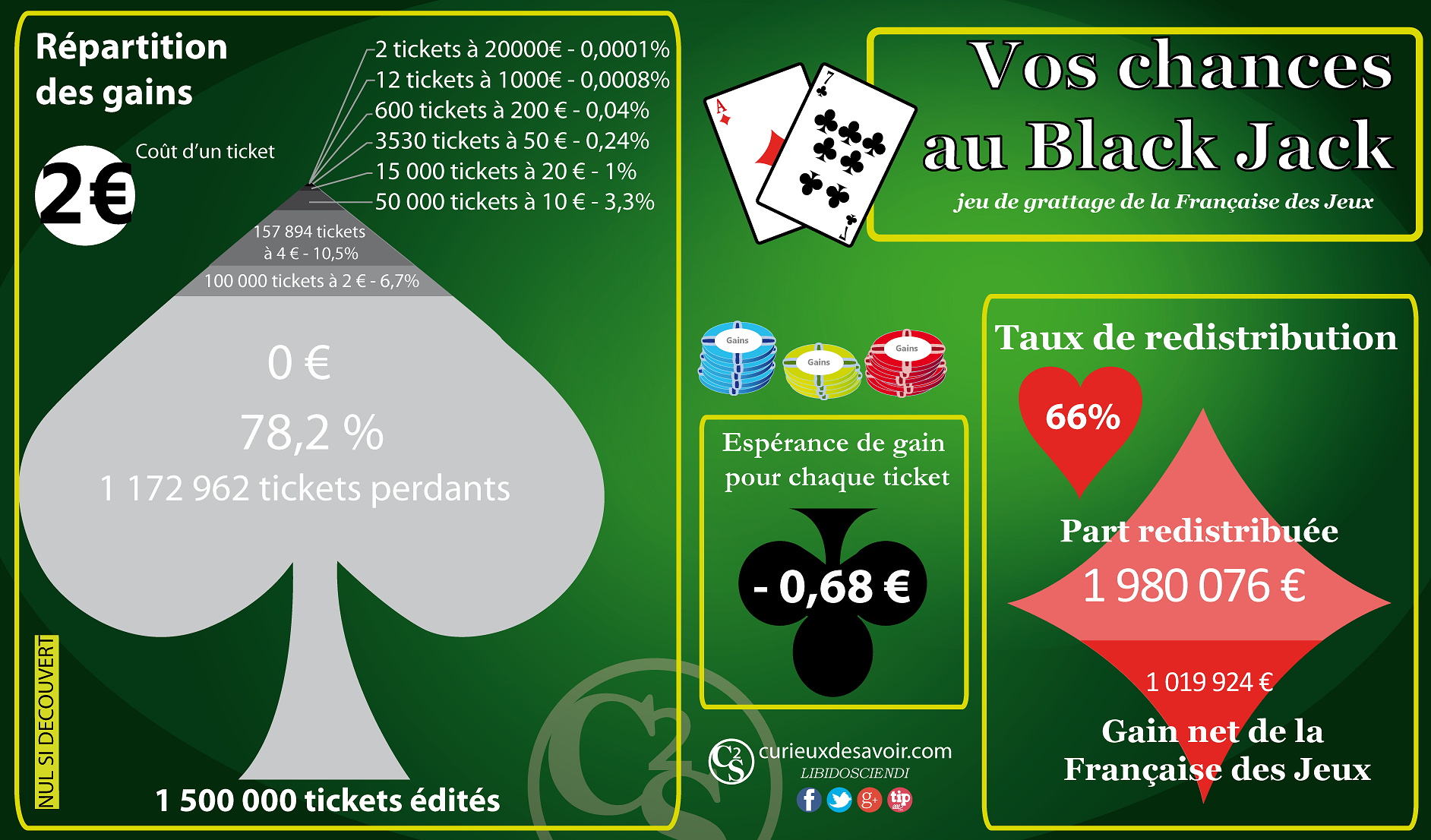
Le black Jack : on perd en moyenne 0,68€ pour chaque ticket acheté
Il est assez cocasse de comparer cette espérance à celles d’autres jeux : « Astro » à 2€ a une espérance de … -0,68€ ! Les jeux de grattage « Banco », « numéro fétiche » et « goal » coûtent 1€. Les gains des tickets gagnants diffèrent : 4 tickets à 1000 € pour « numéro fétiche » contre 2 pour « Banco » et 2 à 2000€ pour « goal ». Cependant, l’espérance de ces 3 trois jeux est strictement la même : -0,37€. Autrement-dit, la Française des Jeux fait en sorte de nous donner autant de chance de perdre de l’argent avec des jeux différents ! Seul le support et la répartition des gains changent.
Donc, si l’on suit la logique mathématique, jouer aux jeux de grattage nous conduit à perdre. Surtout si l’on joue souvent : en s’approchant d’un nombre infini de tirage, la moyenne des gains accumulés se rapproche de l’espérance (voir les lancés de pièces plus haut). Concrètement, en prenant un joueur « régulier », il est quasiment certain que ses gains totaux, ou plutôt ses pertes totales, correspondent à la somme des espérances de l’ensemble des cartes qu’il a achetées. Pour vous en persuader, nous avons fait tourner un petit programme informatique. Nous avons « gratté » au hasard 1 carte, 10 cartes, 1000 cartes, 10 000 cartes, puis 100 000 cartes du jeu « Numéro Fétiche ». Nous avons pris les données fournies par la Française des Jeux pour le jeu « Numéro Fétiche », et fait les tirages en fonction des probabilités réelles. Le tirage est réalisé « avec remise », c’est-à-dire que les probabilités sont toujours les mêmes à chaque tirage. Ce qui implique que l’on «gratte » successivement les cartes de lots de cartes différents.

Plus on achète de tickets, plus on a de chances de gratter un gros lot. Le fait de gagner plus de gros lots en jouant beaucoup peut donner l’illusion aux joueurs de pouvoir se « refaire ». Mais en additionnant ses achats et ses gains, le joueur est de toute façon perdant. En effet, plus on achète de cartes à gratter, plus on se rapproche de l’espérance. L’espérance est la valeur du gain moyen par ticket (ou de la perte lorsqu’elle est négative) si on fait une infinité de grattages.
Alors pourquoi joue-t-on si l’on sait que l’on va perdre ?
D’après l’Institut National de Prévention et d’Education pour la Santé (inpes) et la FDJ, la France comptait en 2010 entre 25 et 28 millions de joueurs réguliers ou occasionnels. Parmi ces joueurs, on classe les très dépensiers (plus de 500€/an), les très réguliers (jouent plus de 1 fois par semaine) et ceux qui sont les deux à la fois (environ 12,2% des joueurs). Il y aurait environ 400 000 personnes présentant des troubles modérés du comportement de jeu et 200 000 avec de grandes difficultés2. Des niveaux proches de ceux relevés aux Etats-Unis où on relève entre 1 et 2% de joueurs pathologiques6.
Les risques liés au jeu
Le jeu compulsif est corrélé avec d’autres comportements à risque2,7-9. Si 3,2% des français présentent des problèmes d’alcoolisme, ils sont 26,5% dans la population des joueurs à risques ! Idem pour le tabagisme, touchant 30% des français contre 64% des joueurs à risque ! Les joueurs les plus préoccupants sont majoritairement des hommes : ils misent plus de 125€ par mois, la moitié d’entre eux ont un revenu mensuel inférieur à 1 100 euros et un tiers n’a pas un seul diplôme2. On a aussi remarqué qu’il existe une relation inverse entre les revenus des personnes et leurs habitudes aux jeux, et ce quel que soit le pays étudié. Les plus pauvres jouent le plus. Mais pourquoi ? On peut bien sûr se poser la question de l’œuf ou de la poule : le jeu entraine-t-il l’alcoolisme, ou est-ce l’inverse ? Il ne semble pas y avoir en réalité une dépendance qui en précèderait une autre. Des personnes seraient plus fragiles à la dépendance7,10 de manière générale car les mécanismes de dépendances sont similaires quel que soit la dépendance11. La génétique12 et le mode de vie en seraient les facteurs déclenchants10.

Dépendances liées aux jeux
Une addiction n’est possible que si l’on y a accès10. C’est logique, mais à y penser, les bars-tabacs où l’on peut jouer à des jeux de hasards sont assez nombreux. Ces dépendances peuvent aussi s’auto-entretenir13,14 : la malchance au jeu peut entrainer un excès d’alcool9, qui lui-même accentuera le jeu etc15. Et comme nous l’avons vu, les personnes prédisposées à l’addiction pourront alors trouver une autre addiction. De nombreuses théories ont été émises concernant le déclanchement de la dépendance, mais il semble que les raisons soient multifactorielles : exclusion sociale, mimétisme de l’entourage, fatalisme, difficultés familiales ou judiciaires en seraient les causes2,5... La question n’est pas encore entièrement élucidé.
Les joueurs pathologiques, les joueurs « raisonnables » et tout autre joueur « lambda » présentent tous des biais cognitifs6,16. Et c’est l’activation de certaines zones du cerveau, indépendamment de notre volonté, qui nous bernerait !17 Un biais cognitif est un mécanisme de pensée qui dévie d’une pensée « purement rationnelle ». Nous en sommes tous victimes, mais les connaître c’est déjà les combattre (lien). Les prix Nobels d’économie Kahneman et Tversky ont été des pionniers pour évaluer ces biais qui nous induisent en erreur. Le biais cognitif le plus marquant pour les joueurs est le biais de distorsion des probabilités. Nous surestimons les probabilités positives par rapport aux probabilités négatives ! Voilà pourquoi un joueur, même s’il sait que le jeu est fait pour qu’il perde, jouera. Cela vaut aussi bien pour les jeux de hasard que dans la vie où nous espérons vivre plus longtemps que la moyenne par exemple. Cela devient bien entendu plus problématique pour le monde de la finance et de l’économie, d’où les travaux de Kahneman et Tversky. Le joueur, addictif ou non, n’est en rien moins intelligent qu’une personne ne jouant jamais ou de manière raisonnable. Il serait victime du biais de distorsion des probabilités comme tous les autres. A un seul détail : le joueur addict aura tendance à plus encore surestimer ses chances18.

Biais cognitif
Manipulations et biais de tous les jours
La publicité de la Française des Jeux le dit : 100 % des gagnants ont tenté leur chance. Le slogan est un pléonasme car « il procède de la répétition synonymique en répétant, à l’aide de mots différents, un même contenu, d’où un apport informatif nul »19. C’est un slogan certainement à prendre au second degré car il est évident qu’il faut jouer pour gagner, mais il révèle un grave problème de perception. En effet, ce slogan laisse à penser qu’il suffit de jouer pour gagner alors que l’espérance de gain des jeux est défavorable aux joueurs. C’est une belle introduction à la pensée critique (voir liens en fin d’article).
Enfin, la médiatisation a un effet dévastateur sur nos petits neurones déjà si fragiles. La mise en avant des gains importants par les petits panneaux « Ici 2000€ gagnés » ou par la médiatisation (reportage TV, émissions etc.) ont un impact direct sur notre perception16,20-22. Les reportages sur le « gagnant du coin » sont une publicité offerte directement par les journalistes en manque de reportage. Quand un joueur est exposé au gain d’une autre personne, et surtout si ce gain est important, ledit joueur prendra plus de risques. Il jouera plus. D’autres études expliquent que le joueur a alors une illusion de contrôle (contrôle du risque et des gains)20.
Conclusion
- Sur toute leur vie, l’écrasante majorité des joueurs perd.
- L’espérance est la valeur moyenne d’un gain pour un ticket.
- Les jeux de hasards présentent tous des espérances en défaveur du joueur.
- Nous sommes tous bernés par des biais qui nous font surestimer nos chances.
- L’exposition et la médiatisation des gains de certains joueurs se traduisent par une incitation à jouer pour les autres.
- Le meilleur moyen de ne pas perde d’argent aux jeux de hasards est de ne pas jouer
- Les joueurs compulsifs sont plus enclins à s’adonner à d’autres comportements à risques (tabac, alcool).
Un merci spécial
A Christina qui a eu l’idée de nous offrir des cartes à gratter (nous avons gagné 8€) sur les 10 que tu as dépensé :-).
Merci à Louis Piquet pour sa relecture attentive et ses idées. Louis est actuellement en Terminale ES à Colmar, et enseigner les maths à Louis fut un plaisir pendant deux ans où quelques idées d’articles germèrent. Louis aime vous tordre les neurones avec ses tours de magie (lien vers sa chaîne youtube).
A lire
En savoir plus sur les biais cognitifs : Associationslibres en podcast Podcastscience et l’argumentation Cortecs. Usez et abusez de ces ressources ! Conseil d’ouvrage : Houdé, O. Le raisonnement: « Que sais-je ? » n° 1671. (Presses Universitaires de France, 2014). Lien
Phosphoré par : Gontier Adrien, Jaeger Catherine
Mots clefs : jeu, grattage, probabilités